Methode der virtuellen Elemente

Es gibt viele unterschiedliche Ansätze zur näherungsweisen Lösung von Problemen mit partiellen Differentialgleichungen in der Kontinuumsmechanik. Dazu gehören Finite-Differenzen-Schemata, Finite-Elemente und Finite-Volumen-Techniken, Randelemente und Partikelmethoden, um nur einige der bekanntesten Diskretisierungsverfahren zu nennen. Mit der Methode der virtuellen Elemente (VEM) wurde eine neue Diskretisierungstechnik eingeführt, die Elemente mit allgemeiner Geometrie - von konvexen bis zu nicht-konvexen Formen - und beliebiger Anzahl von Knoten erlaubt. Aufgrund dieser Allgemeingültigkeit hat VEM im Vergleich zu anderen Methoden mehrere Vorteile, wie

• Zusammenfügen von Vernetzungen mit unterschiedlicher Dichte

• Direkte Einfügung von Rissen in virtuelle Elemente

• Kombination von Phasenfeldansätzen und der direkten Einführung von Rissen bei bruchmechanischen Problemen

• Kontaktberechnungen mit unterschiedlichen Vernetzungen der kontaktierenden Festkörper

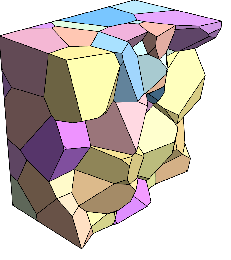
• Modellierung von Mikrostrukturen mit polyedrischen Körnern mit nur einem Element pro Korn

• Erzeugen neuer kontinuierlicher C1-Elemente für Kirchhoff-Platten und -Schalen

• Entfernen von stark verzerrten Elementen in unstrukturierten Netzen

Die Anwendung von VEM auf Probleme der Festkörpermechanik, einschließlich des komplexen elastischen und inelastischen Materialverhaltens, auf Raum-Zeit-Formulierungen und in der Bruchmechanik, wird anhand verschiedener Ansätze im Zusammenhang mit der Methodik der virtuellen Elemente untersucht.