Virtual element methods

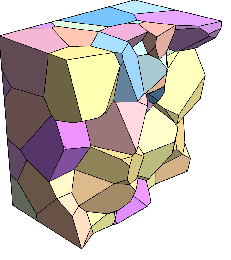
Many different approaches exist for the approximate solution of problems involving partial differential equations in continuum mechanics. These include finite difference schemes, finite elements, finite volume techniques, boundary elements, and particle methods, just to name some of the most prominent discretization techniques. With the virtual element method (VEM), a new discretization technique was introduced that allows elements with general shape from convex to non-convex forms and arbitrary number of nodes. Due to this generality VEM has several advantages when compared with other methods, like

• Treatment of non-matching meshes

• Direct insertion of cracks in virtual elements

• Combine phase field and crack insertion in fracture mechanics

• Treatment of contact with non-matching meshes at the interface

• Model microstructures with polyhedral grains by just one element per grain

• Create new C¹ continuous elements for Kirchhoff plates and shells

• Remove slivers in unstructured meshes using VEM

Application of VEM to solid mechanics problems including complex elastic and inelastic material behaviour, space-time formulations and fracture is investigated using different approaches related to the virtual element methodology.